iMAML笔记（翻译）[更新中]

转载并翻译iMAML的阅读笔记

作者： inFERENCe

本周，我阅读了这份关于元学习的新文章：基于一些关于正则化优化最优结果的微分的观察，与前一版本相比，它的方法略有不同。

• Aravind Rajeswaran, Chelsea Finn, Sham Kakade, Sergey Levine (2019) Meta-Learning with Implicit Gradients

同时发表的另一篇论文也发现了类似的技术，所以我认为我会更新该帖子并提及它，尽管我不会详细介绍它，并且该帖子主要是关于 Rajeswaran et al (2019) 的

• Yutian Chen, Abram L. Friesen, Feryal Behbahani, David Budden, Matthew W. Hoffman, Arnaud Doucet, Nando de Freitas (2019) Modular Meta-Learning with Shrinkage

大纲：

• 我将对元学习设置进行高层概述，我们的目标是学习一种良好的SGD初始化或正则化策略，从而使SGD收敛到更好地完成一系列任务的最小值。
• 我将说明iMAML如何在1D玩具示例中工作，并讨论元目标的行为和属性。
• 然后，我将讨论iMAML的局限性：它仅考虑最小值的位置，而不考虑随机算法最终达到特定最小值的可能性。
• 最后，我将把iMAML与元学习的一种变体方法联系起来。

元学习与MAML

元学习有几种可能的表述方式，我将尝试按照我自己的解释和表示来解释这篇文章的设置，这与这篇文章有所不同，但使我的解释更加清楚（希望会）。

在元学习中，我们有一系列独立的任务，分别具有关联的训练和验证损失函数$f_i$和$g_i$。我们有一组在任务之间共享的模型参数$\theta$，损失函数$f_i(\theta)$和$g_i(\theta)$评估具有参数$\theta$的模型在任务$i$的训练和测试案例中的表现如何。我们有一个算法可以访问训练损失$f_i$和一些元参数$\theta_0$，并输出一些最优或学习的参数$\theta^\ast_i = Alg(f_i,\theta_0)$。元学习算法的目标是关于元参数$\theta_0$优化元目标

$$\mathcal{M}(\theta_0)=\sum_i g_i(Alg(f_{i}, \theta_{0}))$$

在这项工作的早期版本MAML中，该算法被选择为随机梯度下降算法，$f_i$和$g_i$是神经网络的训练和测试损失。元参数$\theta_0$是SGD算法的初始化点，在所有任务之间共享。由于SGD更新是可微的，因此可以通过简单地穿过SGD更新步反向传播来计算相对于初始值$\theta_0$的元目标的梯度。这基本上就是MAML所做的。

但是，初始化对$\theta$最终值的影响非常微弱，并且很难进行分析表征（如果有可能的话）。如果我们允许SGD继续执行许多更新步，则可能会收敛到一个更好的参数，但是轨迹将非常长，并且相对于初始值的梯度将消失。如果我们使轨迹足够短，则关于$\theta_{0}$的梯度是有用的，但我们可能无法达到很好的最终值。

iMAML

这就是为什么Rajeswaran等人选择使轨迹的终点对元参数$\theta_0$的依赖性更强的原因：除了简单地从$\theta_0$初始化SGD之外，他们还通过在loss中添加二次正则项$|\theta−\theta_0|$来固定参数以使其停留在$\theta_0$附近。因此，发生了两件事：

• 现在，SGD的所有步骤都取决于$\theta$，而不仅仅是起始点
• 现在最小化SGD最终收敛到的位置也取决于$\theta_0$

iMAML正是利用了这第二个属性。让我说明一下这种依赖性是什么样的：

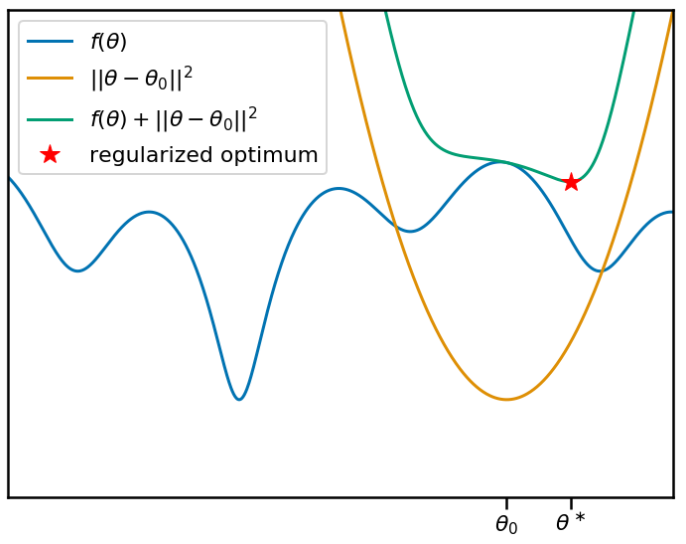
在上图中，假设我们要最小化目标函数$f(\theta)$。这将是元学习算法必须解决的任务之一的训练损失。我们当前的元参数$\theta_0$标记在x轴上，橙色曲线显示了相关的二次惩罚。蓝绿色曲线显示了加上惩罚项的目标。红星表示最小值的位置，这是学习算法发现的位置。

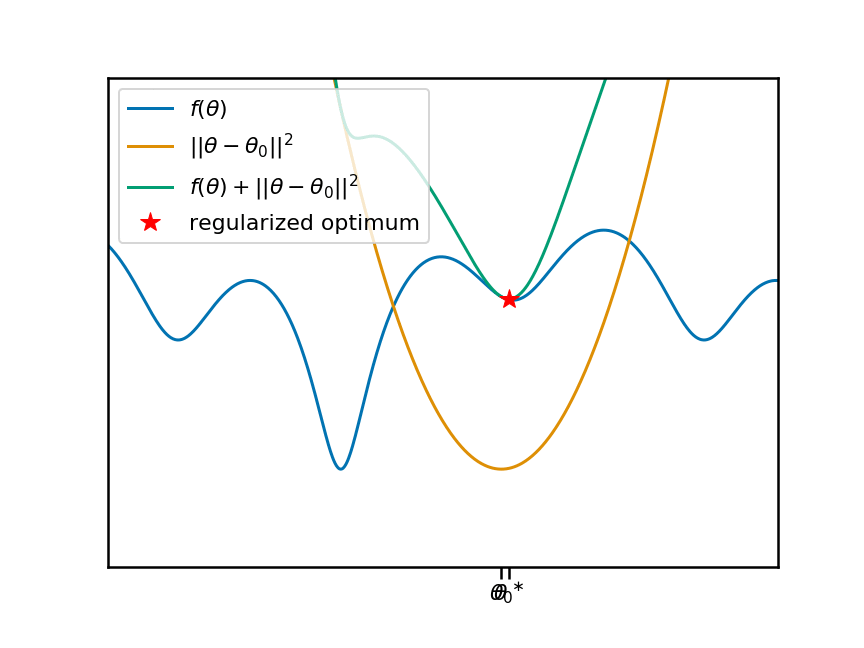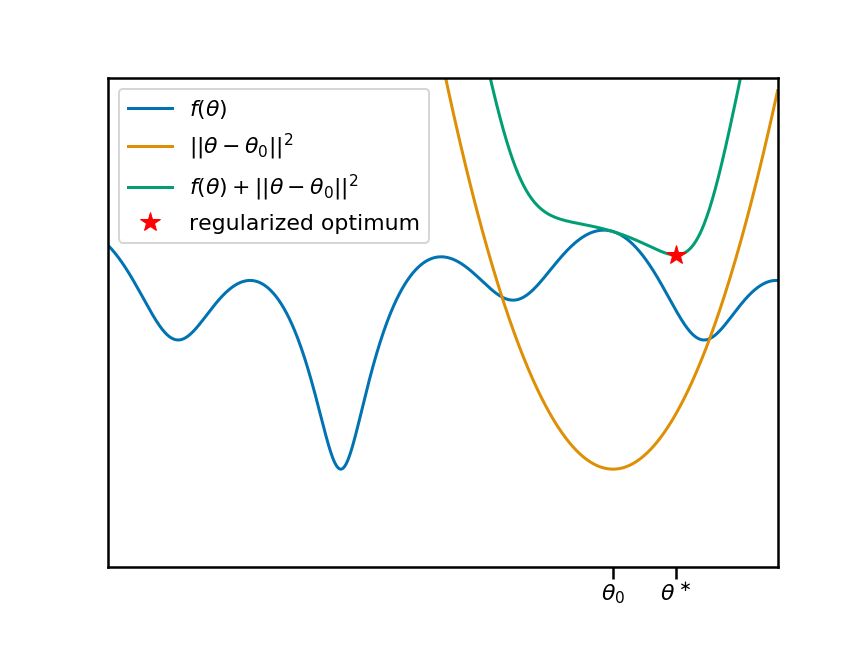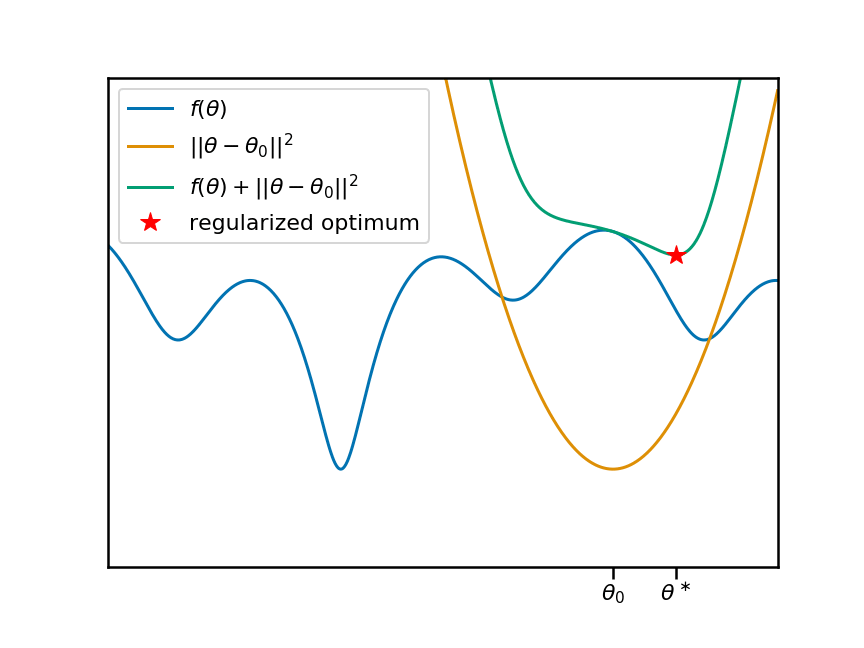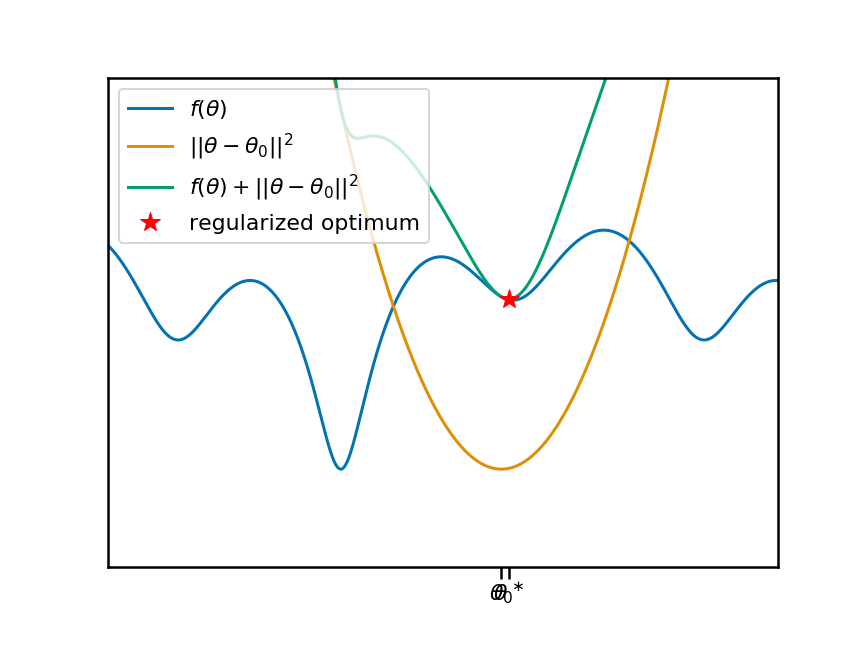
现在，让此动画动起来。我将移动锚点$\theta_0$，并重现相同的图。您会看到，随着我们移动$\theta_0$和相应的惩罚项，正则化目标移动的局部（同时也是全局）最小值发生了变化：

因此很明显，锚点$\theta_0$与局部最小值$\theta^\ast$的位置之间存在非平凡非线性的关系。让我们根据锚点绘制此关系：

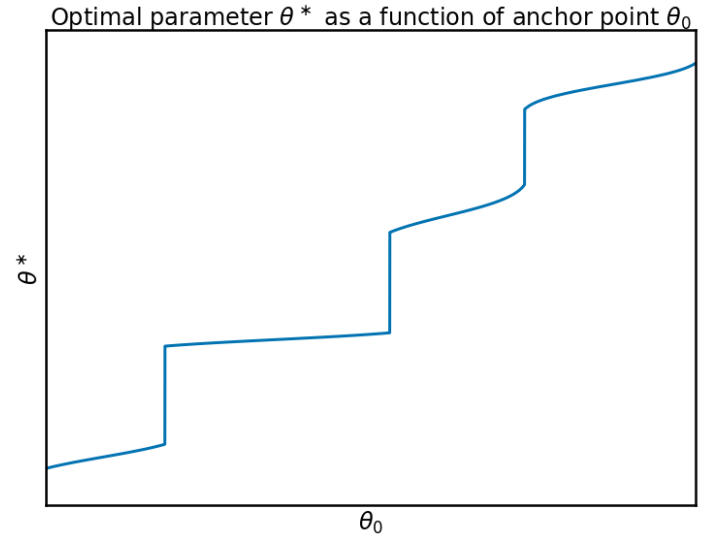
我们可以看到该函数一点也不好处理，当最接近$\theta_0$的局部最小值发生变化时，它具有急剧的跳变，并且在这些跳变之间相对平坦。实际上，你可以观察到最接近$\theta_0$的局部最小值越锐利，则$\theta_0$和$\theta$之间的关系越平坦。这是因为，如果$f$在$\theta_0$附近具有尖锐的局部最小值，则正则化最小值的位置将主要由$f$确定，并且锚点$\theta_0$的位置无关紧要。如果围绕$f$的局部最小值很宽，则最优值会有很大的摆动空间，并且正则化的效果会更大。

Implicit Gradients

现在，我们讨论iMAML程序的全部内容。实际上，该函数$\theta^\ast(\theta_0)$的梯度可以以封闭形式计算。实际上，它与$f$的曲率或二阶导数有关，在我们找到的最小值附近：

$$\frac{d \theta^{\ast}}{d \theta_{0}}=\frac{1}{1+f^{\prime \prime}\left(\theta^{\ast}\right)}$$

为了检查此公式是否有效，我对导数进行了数值计算，并将其与理论预测的结果进行了比较，它们完全匹配：

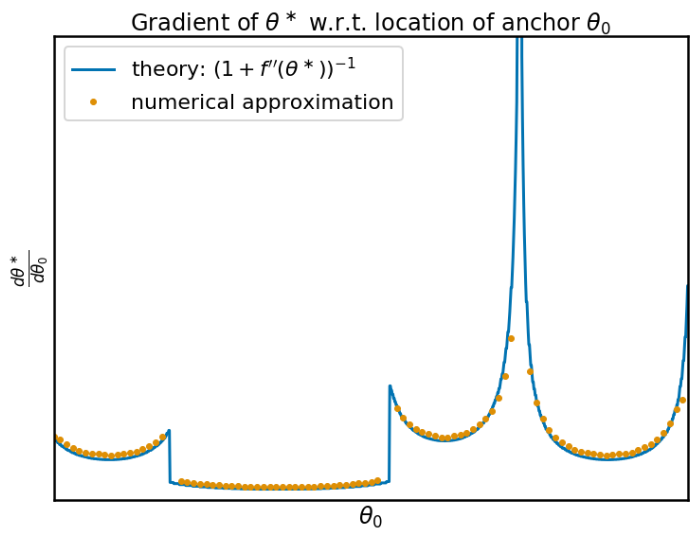
当参数空间是高维时，我们有一个类似的公式，其中包含Hessian的逆加单位阵。在高维中，Hessian的求逆甚至计算和存储都不太实际。iMAML论文的主要贡献之一是使用共轭梯度内部优化循环来逼近梯度的实用方法。有关详细信息，请阅读论文。

Optimizing the meta-objective

在元学习设置中优化锚点时，我们感兴趣的不是位置$\theta^\ast$，而是函数$f$在此位置处取的值。（实际上，我们现在将使用验证损失来代替用于梯度下降的训练损失，但为简单起见，我假设这两个损失是重叠的）。$f$在其局部最优处的值绘制如下：

噢，这个函数不是很漂亮。元目标$f(\theta^\ast(\theta_0))$变成分段连续函数，是相邻盆地之间的连接，边界不光滑。该函数的局部梯度包含很少的有关损失函数的整体结构的信息，它仅告诉你如何到达最接近的局部最小值的位置。所以我不会说这是最好的优化函数。

值得庆幸的是，该函数不是我们必须优化的。在元学习中，我们有优化的函数上的分布，因此实际的元目标类似于$\sum_i f_i(\theta^\ast_i(\theta_0))$。一堆丑陋的函数的总和很可能会变成平滑而优美的东西。另外，我在此博客文章中使用的一维函数不能代表我们要应用iMAML的神经网络的高维损失函数。以模式连通性的概念为例（参见例如Garipov et al, 2018）：似乎SGD使用不同的随机种子发现的模式不仅仅只是孤立的盆地，而是通过训练和测试误差低的光滑的山谷相连。反过来，这可能会使元目标在最小值之间表现得更加平稳。

What is missing? Stochasticity

MAML或iMAML不考虑的重要方面是我们通常使用随机优化算法的事实。SGD不会确定性地找到特定的最小值，而是采样不同的最小值：当使用不同的随机种子运行时，它将发现不同的最小值。

对元目标的更为慷慨的表述将允许使用随机算法。如果我们用$Alg(f_i,\theta_0)$表示算法发现的解的分布，则元目标将是

$$\mathcal{M}_{s t o c h a s t i c}(\theta)=\sum_{i} \mathbb{E}_{\theta \sim \mathcal{Alg}\left(f_{i}, \theta_{0}\right)} g_{i}(\theta)$$

允许随机行为实际上可能对元学习而言是个很好的特性。正则化目标的全局最小值的位置会随$\theta_{0}$突然变化（如上面第三图所示），允许随机行为可能会使我们的元学习目标变得平滑。

现在假设锚定到$\theta_{0}$的SGD收敛到局部极小值的有限集合之一。那么元学习目标以两种不同方式受到$\theta_{0}$的影响：

• 当我们更改锚点$\theta_{0}$时，最小值的位置也会发生变化，如上所述。这种变化是可微的，我们知道其导数。
• 当我们改变锚点$\theta_{0}$时，找到不同解的概率就会改变。有些解的发现频率更高，而有些则更少。

iMAML考虑第一种影响，但它忽略了第二种机制的影响。这并不是说iMAML是错误的，而是它忽略了MAML或通过算法显式微分没有忽略的随机行为可能做出的关键贡献。

Compare with a Variational Approach

当然，这项工作使我想起了贝叶斯方法。每当有人描述二次惩罚时，我所看到的就是高斯分布。

在iMAML的贝叶斯解释中，可以将锚点$\theta_{0}$视为神经网络权重上先验分布的均值。然后，在给定相关数据集的情况下，算法的内部循环或$Alg(f_i,\theta_{0})$会找到$\theta$上后验的最大后验（MAP）近似值。假设损失是某种形式的对数似然。问题是，如何更新元参数$\theta_{0}$？

在贝叶斯世界中，我们将寻求通过最大化边缘似然来优化$\theta_{0}$。由于这通常很棘手，因此通常需要变分近似，在这种情况下，它看起来像这样：

$$\mathcal{M}_{\text {variational }}\left(\theta_{0}, Q_{i}\right)=\sum_{i}\left(K L\left[Q_{i} | \mathcal{N}_{\theta_{0}}\right]+\mathbb{E}_{\theta \sim Q_{i}} f_{i}(\theta)\right)$$

其中$Q_i$逼近任务$i$的模型参数的后验。$Q_i$的特定选择是狄拉克三角洲分布，其中心位于特定点$ Q_i(\theta)= \delta(\theta-\theta^{\ast}_i)$。如果我们慷慨地忽略某些常数会无限大地爆炸，那么高斯先验和简并点后验之间的KL散度就是一个简单的欧几里得距离，而我们的变分目标可简化为：

$$\mathcal{M}_{\mathrm{variational}}\left(\theta_{0}, \theta_{i}\right)=\sum_{i}\left(\left\|\theta_{i}-\theta_{0}\right\|^{2}+f_{i}\left(\theta_{i}\right)\right)$$

现在，该目标函数非常类似于iMAML内循环试图解决的优化问题。如果我们在纯变分框架中工作，则可能是我们留下的东西，我们可以共同优化所有$\theta_i$和$\theta_{0}$。知道的人，请在下面发表评论，为我提供进行元学习的最佳参考。

使用无内环优化或黑魔法，该目标明显易于优化。它只是简单地将$\theta_{0}$拉到更接近为每个任务$i$找到的各种最优值的重心。不确定对于元学习来说这是否是一个好主意，因为通过从头开始从$\theta_{0}$进行SGD，我们可能无法通过共同优化所有目标而获得的$\theta_i$最终值。但是谁知道。鉴于上述观察，一个好主意可能是使$\theta_{0}$和$\theta_i$的变化目标共同最小化，但不时地将$\theta_{i}$重新初始化为$\theta_{0}$。但是在这一点上，我真的只是在编造东西…

无论如何，回到iMAML，它对这个变化目标做了一些有趣的事情，我认为可以将其理解为一种摊销计算：不是将$\theta_i$视为单独的辅助参数，而是指定了$\theta_i$实际上是$\theta_{0}$的确定性函数。。由于变分目标是任何$\theta_i$值的有效上限，因此，如果我们明确地使$\theta_i$取决于$\theta_{0}$，它也是有效的上限。因此，变分目标仅成为$\theta_{0}$的函数（以及算法$Alg$的超参数（如果有的话））：

$$\mathcal{M}_{\text {variational }}\left(\theta_{0}\right)=\sum_{i}\left(\left\|Alg \left(f_{i}, \theta_{0}\right)-\theta_{0}\right\|^{2}+f_{i}\left(Alg\left(f_{i}, \theta_{0}\right)\right)\right)$$

我们终于得到它了。元学习$\theta_{0}$的变分目标与MAML / iMAML元目标非常相似，不同之处在于它还有$|Alg(f_i,\theta_{0})-\theta_{0}|^2$项，这是我们以前没有更新过的$\theta_{0}$的因素。还要注意，我没有使用单独的训练和验证损失$f_i$和$g_i$，但这也是一个非常合理的选择。

这样做的妙处在于，它为iMAML正在尝试做的事情提供了额外的理由和解释，并提出了可能改进iMAML的方向。另一方面，iMAML中的隐式区分技巧可能在其他情况下同样有用，即我们希望摊销后验后验。

我敢肯定我错过了很多参考资料，如果您认为我应该添加任何内容，特别是在变体位上，请在下面评论。

原文链接：Notes on iMAML: Meta-Learning with Implicit Gradients